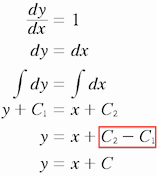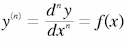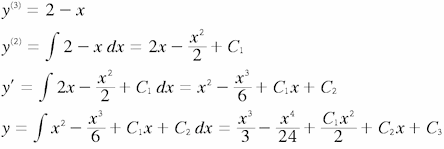Table des matières
Équations différentielles
Exemples d'équations différentielles (ED) :
- Le taux de variation de la vitesse d'un corps en chute libre est proportionnel à son poids, soit
- $\omega$ le poids
- $\upsilon$ la vitesse
- $t$ le temps $$dv_over_dt\varpropto\omega\ \ \ \ \ \ \ dv_over_dt=k\omega$$ où $k$ est la constante de proportionnalité.
- le taux de variation de la température d'un liquide froid laissé dans un environnement chaud, à température constante, est proportionnel à la différence entre les températures. Soit
- $t$ le temps
- $T$ la température du liquide (variable)
- $T_E$ la température de l'environnement (ambiante) $$dv_over_dt\varpropto T_{E}-T\ \ \ \ \ \ \ \ \ dt_over_dt=k\left({T_{E}-T}\right)$$
Rappel
- Dérivation:
- $\left({e^{2x}\cdot\cos\left({3x}\right)}\right)=2e^{2x}\cos(3x)-3e^{2x}\cdot\sin(3x)$
- Trouvons $y'$ pour $e^{x+y}=y\cdot\sin(x)$ : $$y'=e_x_y_-y_cdot_cos_x_over_sin_x_-e_x_y}$$
- Exponentielles et logarithmes: $$\int1_over_4dy=\int1_over_x-2_over_x_5dx}}$$ $$\ln\left|{y}\right|+C_{1}=\ln\left|{x}\right|-2\ln\left|{x+5}\right|+C_{2}$$ $$\ln\left|{y}\right|=\ln\left|{x}\right|-2\ln\left|{x+5}\right|+C_{2}-C_{1}$$ $$\ln\left|{y}\right|=\ln\left|{x}\right|-2\ln\left|{x+5}\right|+C$$ Une constante quelconque plus ou moins une autre constante quelconque donne une autre constante quelconque.
Introduction aux équations différentielles
Définition de base : une équation différentielle (ED) est une équation qui en tient au moins une dérivée, ou au moins une différentielle.
Exemples :
- $d_2_y_over_dt_2}=2\sin(t)dy_over_dt-5t\cdot y$ ⇒ $t$ : variable indépendante et $y$ variable dépendante.
- $\left({5x-3y}\right)dx=(4x+y)dy$ ⇒ ED avec deux différentielles, on ne sait pas quelle variable est dépendante/indépendante.
- $s
-4s'-5s-1$ ⇒ $s$ est la variable dépendante, mais on ne connait pas la variable indépendante. ===== Ordre ===== L'ordre d'une équation différentielle est l'ordre de la dérivée d'ordre supérieure. $$\left({5x-3y}\right)dx=\left({4x+y}\right)dy\rightarrow 5x-3y=\left({4x+y}\right)dy_over_dx$$ $$5x-3ydy_over_dx=4x+y$$ ===== Ordre linéaire ===== Définition : une équation différentielle d'ordre $n$ est linéaire si : - la variable dépendante et ses dérivées ne sont pas multipliés - la variable dépendante et ses dérivées apparaissent seulement au numérateur, affectés de l'exposant 1. - la variable dépendante et ses dérivées ne sont pas l'argument d'une fonction. ===== Homogène ===== Définition : une équation différentielle linéaire est homogène si tous les termes contiennent la variable dépendante ou une dérivée. Autre définition simple : une équation différentielle linéaire est homogène si $f(t)=0$. ===== Coefficients constants ===== Définition : une équation différentielle linéaire est à coefficients constants si les coefficients de la variable dépendante sont constants. ===== Exemples ===== ^ Équation ^ Var. indép. ^ Var. dép. ^ Ordre ^ Linéaire ^ Homogène ^ À coeff. constants ^ | $x+5x'-6x=2\sin(3t)$ | $t$ | $x$ | 2 | oui | non : $2\sin(3t)$ | oui |
| $y^{(3)}+x^{3}y=e^{-2x}$ | $x$ | $y$ | 3 | oui | non : $e^{-2x}$ | non : $x^3$ |
| $y | {(3)}+y | {3}=e | {-2x}$ | $x$ | $y$ | 3 | non | s/o | s/o |
|---|---|---|---|---|---|---|---|---|---|
| $y\cdot{\left({y'}\right)} | {2}+2xy'\cdot y=0$ | $x$ | $y$ | 1 | non | s/o | s/o | ||
| $di_over_dt_2}+4di_over_dt+5i=0$ | $t$ | $i$ | 2 | oui | oui | oui |
Proportionnalité
Solution
Une solution d'une équation différentielle est une expression qui satisfait l'équation différentielle.
Solution particulière : une solution particulière est une solution qui ne contient aucune constante arbitraire. si l'équation différentielle est d'ordre $n$, alors cette solution satisfait $n$ conditions initiales.
Exemple de résolution
Un objet tombe en chute libre à partir d'une hauteur de 18m avec une vitesse initiale de 1m/s. Donnez l'expression de la hauteur de l'objet pendant sa chute. Quand touche-t-il le sol ?
- Vitesse : $v=dy_over_dx$
- $ma=-m\cdot g\ \ \ \ \ \ \ \ \ \ a=dv_over_dt\ \ \ \ \ \ \ \ \ \ dv_over_dt=-g\ \ \ \ \ \ \ \ \ \ d_2_v_over_d_2_t\equiv g=-9,81$
- $y(0)=18\Rightarrow y=18$ si $t=0$
- $v(0)=-1$ (1m/s vers le bas) $\Rightarrow$ si $t=0$ alors $v=-1$.
$$v=\intd_2_y_over_dt_2}dt=\int{-9,81dt}}$$ $$v=dy_over_dt=-9,81+C_{1}$$
Avec la calculatrice : zeros(-4.905*t^2-t+18,t), résultat : {-2.0203 or 1.8164}.
Donc, le temps requis pour l'objet pour atteindre le sol est de 1,8164 seconde.
Solution générale
La solution générale d'une ED d'ordre <m>n</m> est une solution qui contient <m>n</m> constantes arbitraires essentielles.
Exemple:
Avec <m>C_1</m> et <m>C_2</m> on considère qu'une constante additionnée ou soustraite à une autre constante constitue qu'une seule constante.
Peut-on réduire le nombre de constantes arbitraires ? L'expression est solution d'une ED de quelle ordre ?
- x=e-3 (c, Îc) = c. c-'+ 2-3 air, ED d'ordre 1
- x=c, e ⇐ +12 = C, l't. Ci = C,..??-32-t-C, est, est solution du m'En déche L
- x = c, est + C, e-3 t = e-'+ (C, est 1-(e) ⇒ non, solution d'une ED d'ordre 2
Équation différentielle directement intégrable
Une équation différentielle est directement intégrable si elle est de forme, ou peut se ramener à la forme :
Exemple :
Séries de puissance
- Séries de puissance (PDF)