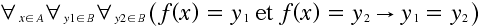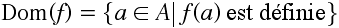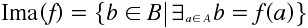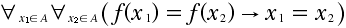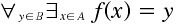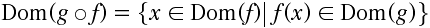Table des matières
Logique
Logique propositionnelle
| Symboles | |
|---|---|
| <html>¬</html> | ¬ |
| <html>∧</html> | ∧ |
| <html>∨</html> | ∨ |
| <html>∀</html> | ∀ |
| <html>∃</html> | ∃ |
| <html>≡</html> | ≡ |
| <html>←</html> | ← |
| <html>→</html> | → |
| <html>↔</html> | ↔ |
| <html>φ</html> | φ |
| <html>ψ</html> | ψ |
| <html>⊕</html> | ⊕ |
Fonctions
Définition : Une fonction <m>f:A right B</m> de l'ensemble <m>A</m> vers <m>B</m> est une règle qui associe à chaque élément de <m>A</m> un et un seul élément de <m>B</m> :
- Le domaine de <m>f</m> est donné par :
- L'image de <m>f</m> est donnée par :
Injective
Définition : Soit <m>f:A right B</m>. La fonction <m>f</m> est injective si
Surjective
La fonction <m>f</m> est surjective si :
Bijective
La fonction <m>f</m> est bijective si elle est injective et surjective.
Fonction composée
Définition : Soit <m>f:A right B</m> et <m>g:B right C</m> deux fonctions. La fonction composée <m>g circ f : A right C</m> est définie par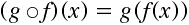 
avec
Fonction inverse
Définition : Soit <m>f:A right B</m> une fonction bijective. L'inverse de <m>f</m> est donnée par la fonction <m>f^-1:B right A</m> définie par <m>f^-1(b)=a</m> si et seulement si <m>f(a)=b</m>.
Proposition 1 : Soit <m>f:A right B</m> une fonction bijective. On a <m>f^-1 circ f=I_{A}</m> et <m>f circ f^-1=I_{B}</m> où <m>I_{A}:A right A</m> et <m>I_{B}:B right B</m> désignent respectivement les fonctions identité des ensembles <m>A</m> et <m>B</m>.